Partición Binaria del Espacio
linkAlgoritmo BSP
Particionamiento del espacio binario (BSP) es un método para subdividir recursivamente un espacio en elementos convexos empleando hiperplanos. Este proceso de subdivisión da lugar a una representación de objetos dentro del espacio en forma de un estructura de datos de árbol conocido como Árbol BSP.
La partición binaria del espacio es un proceso genérico que divide una escena recursivamente en dos hasta que satisface uno o más requisitos. El método específico empleado varía dependiendo del objetivo final. Por ejemplo, en un árbol BSP empleado para la detección de colisiones el objeto original sería dividido hasta que cada parte sea lo suficientemente sencilla como para ser individualmente comprobada, y en el renderizaje interesa que cada parte sea convexa, de forma que el algoritmo del pintor pueda ser usado posteriormente.
Un árbol BSP es una estructura de datos utilizada para ordenar y buscar polígonos en el espacio n-dimensional. El espacio es representado por el árbol, mientras que los nodos del mismo representan subespacios convexos. Cada nodo almacena hiperplanos que dividen el espacio en dos, referencian a dos nodos y almacenan uno o más segmentos o polígonos (según las dimensiones del espacio utilizado). Normalmente los árboles BSP representan espacios de dos dimensiones (juegos tipo Doom) y tres dimensiones (juego tipo Quake). En el primer caso los nodos almacenan segmentos y en el segundo los nodos almacenan polígonos.
La siguiente imagen ilustra el proceso de partición de un polígono irregular en una serie de polígonos convexos. Destacar cómo cada paso produce polígonos con menos segmentos hasta que se llega a F y G, que son convexos y no necesitan mayor partición. En este caso en particular, la línea de partición se ha tomado empleando vértices existentes del polígono y no se intersecciona con ninguno de sus segmentos. Si la línea de partición se intersecciona con un segmento, o una cara en un modelo tridimensional, el/los segmento/s o cara/s tienen que ser divididas en dos dado que cada partición debe ser un objeto completo e independiente.
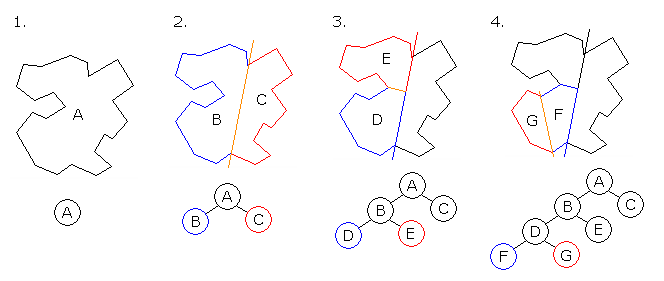
- A es la raíz del árbol y de todo el polígono.
- Se divide A en B y C
- Se divide B en D y E.
- Se divide D en F y G, que son convexos y se convierten en hojas del árbol
linkObjetivos del BSP
- Permiten determinar el orden en que deben ser dibujados los polígonos para lograr el retiro superficial ocultado.
- Permiten determinar si un punto determinado está en una parte sólida del modelo o no.
- Permiten detectar las colisiones con el modelo.
linkUsos del BSP
Inicialmente, esta idea se propuso para los gráficos 3D por ordenador para incrementar la eficiencia de renderizado. Otros usos son el procesamiento geométrico con formas, Constructive Solid Geometry en herramientas CAD, detección de colisiones en robótica y videojuegos 3D, y otras aplicaciones informáticas que incluyen el manejo de estructuras espaciales complejas. la eliminación de caras ocultas ya que gracias a los planos divisorios del árbol conoceríamos qué polígonos están detrás o delante, teniendo solamente que considerar determinadas ramas del árbol a través de la posición desde la que nos estemos posicionando en él.

El uso más común de los árboles de BSP es probablemente retiro superficial ocultado en tres dimensiones. Los árboles de BSP proporcionan un método elegante, eficiente para clasificar polígonos vía una primera caminata del árbol de la profundidad: algoritmo “del pintor delantero” o Algoritmo del pintor.
linkSolución y Resultados
| No. | Descripción |
|---|---|
| 1 | Crear el nodo raíz. |
| 2 | Dividir el área a lo largo de una línea horizontal o vertical. |
| 3 | Seleccionar una de las dos nuevas celdas de partición. |
| 4 | Realizar nuevamente el paso numero 2 (usando esta celda como el área a dividir). |
| 5 | Dividir el área a lo largo de una línea horizontal o vertical. |
| 6 | Realizar todos los pasos nuevamente hasta que cada parte sea lo suficientemente sencilla como para ser individualmente comprobada. |
1linkvar imported = document.createElement('script');
2linkimported.src = "/vc/docs/sketches/workshop3/node.js";
3linkdocument.head.appendChild(imported);
4link
5linkvar height = 720;
6linkvar width = 1280;
7link
8linkvar mouseStartPos;
9linkvar mouseEndPos;
10linkvar auxPoint;
11linkvar toDraw = false;
12link
13linkvar pressedMouseLine = null;
14link
15linkvar initialVertices = [[0,0],
16link [width, 0],
17link [width, height],
18link [0, height]]
19linkvar rootNode;
20link
21linkfunction setup() {
22link createCanvas(1280, 720);
23link mouseStartPos = createVector(0,0);
24link mouseEndPos = createVector(0,0);
25link auxPoint = createVector(0,0);
26link rootNode = new Node(initialVertices, null, null);
27link}
28link
29linkfunction draw() {
30link clear();
31link stroke(255,255,255);
32link strokeWeight(4);
33link rootNode.draw();
34link if (pressedMouseLine != null){
35link line(pressedMouseLine[0], pressedMouseLine[1], pressedMouseLine[2], pressedMouseLine[3])
36link }
37link}
